ANDMEBAASIDE PROJEKTEERIMISEST, LÜHIDALT (Ⓒ Inga Petuhhov, TLÜ DTI 2019)

SISSEKANNE # 91

ANDMED JA ANDMEBAAS

Andmed (data) - informatsiooni taastõlgendatav esitus formaliseeritud kujul, mis sobib edastuseks, tõlgenduseks või töötluseks. Samuti: toormaterjal, mis on mingil viisil kogutud.

Informatsioon (information) - teadmus, mis puudutab objekte, näiteks fakte, sündmusi, asju, protsesse või ideid, sealhulgas mõisteid, ja millel on teatavas kontekstis eritähendus.  Samuti: toormaterjal töödeldult ja organiseeritult, tal on tähendus. 

Teadmised (knowledge) – kogutud info põhjal tehtud järeldused ja üldistused.

Andmebaas (database) on kogum omavahel seostatud andmeid. Andmebaasi (AB) omadused:

→    esindab mingit osa tegelikust maailmast;

→    on loogiliselt sidus ja tähendusega andmekogum;

→    on loodud kindla eesmärgiga ja on vajalik kasutajatele mingite eesmärkide saavutamiseks;

→    koos andmetega hoitakse andmete struktuuri ja koosluse kirjeldust.

 

ACID

ACID kui näide sellest, milliste probleemidega tuleb muuhulgas tegeleda andmetega töötamisel. ACID (Atomicity, Consistency, Isolation, Durability) – omaduste kogum, mis on oluline andmebaasis tehtavate tehingute puhul, mis peavad tagama andmete kehtivuse andmebaasis ka peale võimalikke probleeme, vigu jms. Eesti keeles:

·         Atomaarsus – AB tehing on üks nn atomaarne üksus – ta kas viiakse lõpule tervikuna või ei tehta üldse. Mitte mingeid andmebaasi vaheseise ei tohi muu maailm näha (raha ülekanne ei või jääda poolikuks).  

·         Konsistentsus – Andmebaasi korrektsed olekud on määratud piirangutega, reeglitega. AB tohib muutuda ühest lubatud olekust teise (kui tehakse baasis tehingut, siis tulemust tohib näha alles siis, kui kõik on tehtud, vahepealsed olekud ei ole väljapoole nähtavad).

·         Isoleeritus – kui ka tehingud toimuvad paralleelselt, peab nendel olema sama tulemus järjest toimuvate tehingutega (samaaegsed tehingud sama kontoga annavad sama tulemused, kui nad toimuksid järjest)

·         Püsivus - kui tehing on lõppenud, peab olema tagatud, et tulemused on sellised, nagu nad tekkisid, AB peab taastuma võimalikest tekkivatest vigadest.

 

ANDMEBAASIHALDUSE SÜSTEEMID (ABHS)

Andmebaasihalduse süsteem (database management system - DBMS) on enamasti üsna keerukas tarkvara, mis paikneb andmete ees, vahendades rakenduste jaoks ligipääsu andmetele ning tagades samal ajal mitmete omaduste täidetust nii andmete kui ka nendele ligipääsu osas. ABHS täidab järgmisi ülesandeid:

→     On võimeline salvestama andmeid.

→     Tagab andmete kestvuse / püsivuse.

→     Annab vahendid soovitud andmete kiireks väljaotsimiseks.

→     Tagab turvalisuse.

→     Võib ka aidata leida andmetes mustreid ja arengusuundi.

ABHS FUNKTSIOONID: ABHS peab aitama andmebaasiga olulisi tegevusi läbi viia. AB loomine, kustutamine, haldamine – AB struktuuri loomine ja muutmine, kasutajate loomine ja õiguste andmine, andmete varundamine ja taastamine. AB kasutamine => Andmete lisamine, muutmine, kustutamine, päringute tegemine, protseduuride käivitamine.

Milleks andmebaasid?  Andmebaase ei tehta reeglina andmebaasi enda pärast. Andmebaasid peavad aitama lahendada ülesandeid, kus on tarvis tegelda suurema koguse andmetega. Nad on osaks paljudes veebirakendustes, sotsiaalmeedias, ettevõtete infosüsteemides, raamatupidamisprogrammides, personaliarvestuses jne. Andmebaasid luuakse koos neid kasutava tarkvaraga ja nii on see tegevus tihedalt seotud üldise tarkvaraarendusega.

TARKVARAARENDUS

Tarkvaraarendust “tükeldatakse” faasideks / tegevusteks mitmel erineval viisil. Üks võimalusi on järgmine:

→     Nõuete analüüs ja kirjeldamine

→     Tarkvara kavandamine

→     Realisatsioon ja moodulite testimine

→     Integratsioon ja süsteemi testimine

→     Kasutamine ja hooldus.

Kuhugi siia sisse peab tihtipeale mahtuma ka andmebaasiga tegelemine. Järgmisel slaidil on joonis R. Elmasri, S. Navathe raamatust, mis näitab tarkvara arendust rõhuga andmebaasidele.

Elmasri, R & Navathe, S. Fundamentals of Database Systems. 6th ed.

Jooniselt on näha kaks olulist tegevust andmebaasi loomisel: 1) kontseptuaalne disain: tulemuseks kontseptuaalne (mõiste) mudel (üldine) 2) loogiline disain: tulemuseks loogiline/tehniline

andmemudel, realisatsioonimudel (andmebaasi tüübi jaoks spetsiifiline). 

Disain on siin kontekstis kavandamine ehk projekteerimine (mitte kaunistamine / kujundamine). Kavandamise tulemuseks on mudelid, mida ingl keeles siin kontekstis tavatsetakse schema’deks kutsuda. Andmebaasi kavandamine on tegeliku elu mõistete /andmete ja nende vaheliste suhete komplekti panemine parimal võimalikul kujul andmebaasi.

MUDEL JA ANDMEMUDEL

Mudel on tegelikkuse lihtsustatud kirjeldus, mis toob välja olulise ja jätab kõrvale ebaolulise. Oluline ja ebaoluline on suhteline ja sõltub kontekstist. Mudel peab olema täpne ning esitatud arusaadavalt sellele “seltskonnale”, kelle jaoks seda vaja on. Mudel võib olla kirjeldatud tekstina, kuid tihti on abiks joonis. Modelleerimine on mudeli koostamine.

Andmemudel (data model) on mõistete ja põhimõtete süsteem, mille abil saab kirjeldada andmestiku ülesehitust, andmeelementide omavahelisi seoseid. Meie kontekstis on andmemudeleid vaja andmete struktuuri ja seoste kirjeldamiseks ning teisalt konkreetse andmebaasi struktuuri kirjeldamiseks (andmetüübid, seosed, kitsendused). Andmemudelisse võivad kuuluda ka põhioperatsioonid andmete manipuleerimiseks ning võimalus täiendavaid operatsioone kirjeldada.

Andmemudeli kategooriad => Jaotus vastavalt tasemele, millel andmeid kirjeldatakse:

·         Kontseptuaalne andmemudel (conceptual data model) – kõrgema taseme mudel, mis annab vahendid andmete kujutamiseks nii, nagu kasutajad neid tajuvad.

·         Füüsiline andmemudel (physical data model) – madala taseme mudel, annab vahendid, et kirjeldada andmete salvestamist (kõva)kettal.

·         Tehniline andmemudel (representational data model) – jääb eelnevate vahele ja annab andmete kirjeldamiseks vahendid, mis on arusaadavad kasutajale, kuid teisalt ei ole liiga kaugel andmete salvestamisest.

Andmemudelid, mida on kasutatud ja kasutatakse andmebaasihalduse süsteemides: 

Pärandandmemudelid (legacy data models):

→     Hierarhiline andmemudel (1960ndad, IBM) – vanim AB struktuur, andmete vahel on puukujulised seosed – üks vanem, mitu last. Inkarnatsioon XML-s.

→     Võrkmudel (1960ndate lõpp) – püüdis parandada eelmise jäikust, kuid kaotas populaarsuses relatsioonilisele mudelile. Tänane graafimudel on mingis mõttes järglane.

→     Relatsiooniline (nn SQL) andmemudel (1970ndad, Edgar F. Codd)

→     Isekirjeldavad andmemudelid, dokumendiandmebaasid, NoSQL süsteemid. Andme-mudelite alusel on loodud andmebaasihalduse süsteemid, mis toetavad vastavat tüüpi andmebaase. Näiteks relatsioonilised andmebaasisüsteemid vastavad relatsioonilisele andmemudelile.

Praktikas nimetatakse andmemudeliks tihti konkreetse andmebaasi kirjeldust (struktuuri).

Andmemudel (data model) on andmebaasi ülesehituse kirjeldus. Rohkem kasutatakse siiski mõistet andmebaasi struktuur või skeem (schema). Andmebaasi struktuuri kirjeldamisel lähtutakse andmebaasi tüübist ning vastavast andmemudelist (meie kasutame relatsioonilist mudelit). Andmebaasi kirjeldus ja andmebaas on erinevad mõisted.

KONTSEPTUAALNE ANDMEMUDEL

Kontseptuaalne andmemudel, ka infoloogiline mudel (conceptual data model) on mittetehniline mudel, mis kirjeldab valdkonna põhiandmeid, nõudeid säilitatavatele andmetele. Kontseptuaalne andmemudel on lakooniline kirjeldus kasutajate nõuetest andmetele, sisaldades olemitüüpe (entity types), seoseid (relationships) ja kitsendusi (constraints). See mudel ei tegele realisatsiooni detailidega (andmebaasihalduse süsteem, riistvara, arvutivõrk, töökiirus, …). Mudeli jaoks sobib visuaalne esitus. Kontseptuaalne mudel on aluseks tehnilisema(te)le mudelitele – näiteks mudelile, mille järgi andmebaas luua.

 

OLEM-SEOS MUDEL

Olem-seos mudel (entity-relationship model) – kõrgema taseme kontseptuaalne mudel, kus kirjeldatakse olemeid, nende (olulisemaid) omadusi ja seoseid olemite vahel. Mudeli abil kirjeldatakse omavahel seotud asju, mis jäävad huvipakkuvasse valdkonda, nn minimaailma.

Olem (entity) – kirjeldab reaalselt eksisteerivaid sõltumatuid asju või objekte, mõisteid, nähtusi ja on selle üldmõisteks. Olemil on atribuudid (attributes), mis kirjeldavad olemit lähemalt, esitades meie jaoks huvitavaid olemi omadusi. Üldjuhul on igal olemi atribuudil väärtus.

Seos (relationship) – side või ühendus (association) kahe või enama olemi vahel. Olemite ja seoste modelleerimisest kirjutab Peter Chen 1976. a artiklis  "The Entity-Relationship Model - Toward a Unified View of Data".

OLEMID JA ATRIBUUDID

Eristada tuleks (ideaalis) mõisteid olem ja olemitüüp.

Olemitüüp (entity type) on sarnaste olemite üldine kirjeldus, mida saab kanda mudelisse. Vrdl andmetüüp.

Olem on konkreetne reaalsuses eksisteeriv objekt, mõiste vms, mis vastab mingile olemitüübile. Vrdl muutuja.

Olemihulk on kõik andmebaasis olevad samale olemitüübile vastavad olemid. Alternatiivselt on kasutusel ka mõisted: olem (üldine kirjeldus) ja olemi eksemplar / olemi isend (konkreetne objekt vms).

Olemitüübiga koos kirjeldatakse atribuudid (attributes). Konkreetse olemi puhul on atribuudil väärtus, näiteks kui olemitüübil on atribuut "nimi", siis selle väärtuseks võib olla "Maali Maasikas". Atribuudile kehtestatakse väärtuste osas kitsendused – määratakse väärtuste hulgad. Sisuliselt on tegemist andmetüübiga. Atribuudid võib jagada erinevatesse kategooriatesse:

→     lihtatribuudid (simple) või liitatribuudid (composite attributes);

→     üheväärtuselised (single-valued) või mitmeväärtuselised (multi-valued) atribuudid;

→     salvestatud (stored) või tuletatud (derived) atribuudid.

Lihtatribuudil saab olla üks, jagamatu väärtus: näiteks olemil õppeaine on atribuut nimetus. nimetus = "Andmebaaside projekteerimine".

 Liitatribuudi väärtus koosneb mitmest osast, kus iga osa väljendab mingit väiksemat tähendusega omadust. Näiteks atribuut aadress on üpris keerukas nähtus, koosnedes postiindeksist, maakonnast, linnast / alevikust / ..., tänavast, majanumbrist ja korterinumbrist. Liitatribuute kasutatakse siis, kui on vaja vastavat atribuuti kasutada mõnikord terviklikult, teine kord aga vaid mingit osa (nt maakond). Liitatribuutide puhul tuleb tihti lahendada küsimus, kuidas seda mõistlikult salvestada.

Enamasti on atribuudid üheväärtuselised. Näiteks olemitüübi õppeaine atribuut nimetus Mõnel atribuudil võib olla (kuid ei pruugi) mitu väärtust, sel juhul on tegemist mitmeväärtuselise atribuudiga. Näiteks võib inimesel olla üks hobi või mitu hobi. Auto võib olla värvitud ühte värvi või mitmesse erinevasse värvi. Mitmeväärtuselise atribuudi jaoks võivad olla kehtestatud piirarvud väärtuste hulgale – nt auto võib olla värvitud maksimaalselt kolme erineva värviga.

Enamus atribuute on nn salvestatud atribuudid. Mõne atribuudi väärtus on võimalik tuletada või arvutada teise atribuudi väärtuse kaudu. Need ongi tuletatud atribuudid. Näiteks isiku vanus, mida saab leida isiku sünnikuupäeva (salvestatud atribuut) ja tänase kuupäeva järgi. Tuletatud atribuudi väärtuse võivad määrata ka teised olemid (olemitüübid) – näiteks kursusele registreerunud üliõpilaste arv.

Osa atribuute on erilised – need on võtmeatribuudid ehk võtmed (key attributes). Võtmeteks nimetatakse selliseid atribuute, millel on kõigi antud tüüpi olemite hulgas unikaalne (ühene, ainuline) väärtus. Öeldakse ka nii, et ühes olemihulgas olevatele olemitele kehtib võtme unikaalsuse kitsendus, s.t. peab olema mingi atribuut, mida saab kasutada olemi üheseks identifitseerimiseks. Ka mitu tavalist atrubuuti koos võivad moodustada võtme ja olla unikaalne.

Olemitüübil võib võtmeks sobiv atribuut puududa, seda nimetataks nõrgaks olemitüübiks.

 

MUDELITE ESITAMINE

Kontseptuaalse ja realisatsioonimudeli (tehnilise mudeli) esitamiseks olem-seos diagrammina võib kasutada erinevaid skeemitüüpe. Võimalikud variandid relatsioonilise andmebaasi puhul:

→     UML klassiskeem (UML class diagram) sobib mõlema mudeli jaoks, erinevus on mudeli detailides.

→     Varesejala notatsioon (Crow's foot notation) sobib samuti mõlemale mudelile.

→     Cheni notatsioon sobib kontseptuaalseks mudeliks. Realisatsiooni mudeli jaoks on vaja teistsugust skeemitüüpi.

NÄIDE OLEMITEST JA ATRIBUUTIDEST

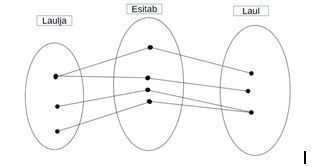
Rakendus: Laulja ja laul. Hetkel ei ole täpsustatud, mida selles rakenduses peaks teha saama, ehkki võiks olla (lauljat esinema tellida?, lauludest teatud pikkusega ja mingis stiilis kava kokku panna?, ...)

·         Laulja andmed näiteks: artistinimi, pärisnimi, esineja tüüp (üksi, bändiga), muusikastiil, mänedžeri nimi, esinemistasu, …

·         Laulu andmed näiteks: pealkiri, muusika autor, sõnade autor, pikkus, stiil, loomise aasta, esitaja, …

Järgnevatel joonistel  näited nendest kahest olemist erinevaid tähistusi kasutades.

 

 

 SEOSED JA SEOSTE STRUKTUURSED KITSENDUSED

Olemitüübid (ja koos sellega olemid) on üksteisega seotud, viidates üksteisele (laulul on esitaja). Olem-seos-mudelis ei tohiks viiteid ühest olemitüübist teisele teha atribuutide abil (olemitüübis laul on atribuut esitaja / laulja), vaid selleks kasutatakse seoseid (relationship).  

Seosetüüp (relationship type) kirjeldab sidemete hulga (set of associations) erinevate olemitüüpide vahel. Need on seosed konkreetsete olemite vahel erinevatest olemitüüpidest. Seosed võivad olla ka samasse olemitüüpi. Näiteks seos konkreetse laulja ja konkreetse laulu vahel.

 

Seostele kirjeldatakse struktuursed kitsendused (structural constraints), mis määravad võimalikud kombinatsioonid, kuidas olemid võivad osaleda vastavas seoses. Binaarse seose (seos kahe olemi vahel) võimsustik (cardinality ratio, multiplicity) määrab maksimaalse arvu seose eksemplare, milles üks olem osaleda saab. Lubatud võimsustikud on: 1:1, 1:N, N:1 ja M:N. Näited:

→     M lauljat esitavad N laulu (laulja võib esitada erinevaid laule ja sama laulu võivad esitada erinevad lauljad) (M:N)

→     Ühel õppekaval õpib palju (N) üliõpilast (1:N)

→     Üks üliõpilane saab ühe diplomi  (1:1).

Osalemise kitsendus (participation constraint) määrab minimaalse arvu seoseid, milles vastav olem osalema peab. Eristatakse täielikku (total) ja osalist (partial) osalemist.

→     Täieliku osalemise korral olem eksisteerib vaid siis, kui ta osaleb seoses. Näiteks iga üliõpilane on kindlasti seotud mõne õppekavaga.

→     Osaline osalemine ei nõua kõigi olemite osalust vastavas seoses. Näiteks mõnel laulul ei pruugi olla esitajat.

Seosetüübil võivad sarnaselt olemitüüpidele olla atribuudid. Atribuudid kirjeldavad seost, näiteks olemite vahelise suhte tekkimise algust ja lõppu, täpsemat suhte tüüpi jne. Seosetüübis on reeglina vaja atribuutide abil ka määrata, millised konkreetsed olemid selles seoses osalevad ning võivad olla atribuudid, mis on kuidagi mõlema olemiga seotud – nt kuupäev, millal laulja konkreetset laulu esitas. Seostel võivad olla rollinimed, mida saab kasutada seose tähenduse täpsustamiseks. Olemitüüp võib läbi seose olla seotud iseendaga. Sel juhul tegemist on rekursiivse seosega.

NIMEDEST JA NIMETAMISEST

Mudeli mõistetavuse huvides tuleb anda kõigile mudelis olevatele "osadele" läbimõeldud nime. Nimed peavad olema kooskõlas valdkonnaga. Olemite nimed on nimisõnad ja on ainsuses. Seoste nimed on enamasti seotud tegevusega ja tulenevad tegusõnadest. Olemite ja seoste nimed kirjutatakse tihti läbivalt suurtähtedega. Nõudeid kirjeldava jutustuse alusel pannakse nimisõnad tavaliselt olemiteks ja tegusõnadest tuletatakse seosed. Atribuudid on nimisõnad, mis kirjeldavad olemeid. Inglise keeles on soovitavalt olemite ja seoste nimedest võimalik moodustada lauseid: Singer (olemitüüp) performs (seosetüüp) song (olemitüüp).

 

OLEM-SEOS MUDEL JA RELATSIOONILINE MUDEL

 

Olem-seos mudeli all on järgnevas mõeldud nn Chen’i märgisüsteemiga esitatud mudelit koos olemite, atribuutide ja olemite-vaheliste seostega (nn kontseptuaalne mudel).

Relatsiooniline / tehniline andmemudel peaks vastama sisuliselt andmebaasistruktuurile (representational model). Relatsiooniline andmemudel sõltub reeglina konkreetsest andmebaasi haldussüsteemist

Kogenud analüütik enamasti Chen’i mudelit eraldi ei joonista, sest ta suudab tekkivad probleemid peas läbi töötada.

Teisendamisel tehtavad soovituslikud sammud aitavad loodetavasti probleeme paremini tajuda ja lahendada.

Relatsioonilise andmemudeli põhimõtteid kirjeldas esimest korda 1970. a inglise arvutiteadlane  Edgar Frank “Tedd” Codd:  artikkel “A Relational Model of Data for Large Shared Data Banks” https://www.seas.upenn.edu/~zives/03f/cis550/codd.pdf.

Mudeli teoreetilised alused on matemaatikas: hulgateoorias ja predikaatloogikas. Esimesed relatsioonilise mudeli realisatsioonid andmebaasihalduse süsteemides tulid 1980-te alguses (IBM SQL/DS ja Oracle andmebaasihalduse süsteem).

Relatsiooniline mudel (relational model) kirjeldab andmebaasi kui relatsioonide kogumit.  Relatsioon (mis on teoorias ametlik mõiste) on teisisõnu väärtuste tabel.  Iga rida (kirje) tabelis on omavahel seotud väärtuste hulk, esindades  midagi reaalsest maailmast (vrdl olemiga). 

 Ametlik mõiste rea jaoks on ennik või korteež (tuple). Tabeli veergude päised (nimed) on vajalikud igas reas olevate väärtuste tõlgendamiseks. Veerunimede ametlik mõiste on atribuut (attribute). 

Andmetüübi abil kirjeldatakse iga veeru jaoks lubatud väärtuste hulk. Seda nimetatakse domeeniks (domain).

Domeen on lubatud väärtuste hulk, kusjuures väärtused ei ole jagatavad väiksemateks osadeks (atomic values). Nad on atomaarsed. Võimalik tõlge sõnale domain on ka määramispiirkond, mis sobib konteksti hästi. Enamasti määratakse domeen andmetüübi abil, mille hulgast väärtused pärinevad (vanus pärineb täisarvude hulgast). Domeenil on nimi, mis selgitab tema olemust – näiteks Eesti isikukood on 11 numbrist koosnev ja teatud reeglitele vastav numbrijada. Domeenile võib olla määratud spetsiifiline formaat – näiteks TLÜ üliõpilaskoodi tähtede-numbrite “süsteem” - kuidas seda võiks kirjeldada?

VÄÄRTUSED JA NULL’id

Enniku (tabeli rea) iga väärtus on relatsiooniteooria kohaselt atomaarne ehk ei ole jagatav. Järelikult liitatribuudid ja mitmeväärtuselised atribuudid ei ole relatsioonilises mudelis lubatud. Tavaliselt jagatakse liitatribuut mitmeks atribuudiks. Mitmeväärtuselised atribuudid saavad endale eraldi tabeli (relatsiooni) Sellistele reeglitele vastavat mudelit kutsutakse ka lamedaks relatsiooniliseks mudeliks (flat relational model).

Relatsioonides võivad esineda NULL-väärtused, mis tähendab tegeliku väärtuse puudumist, NULL võib tähistada kolme olemuselt erinevat olukorda:

·         Väärtus on teadmata (üliõpilane ei soovi avaldada oma aadressi);

·         Väärtus on olemas, kuid ei ole hetkel kättesaadav (mis iganes väärtuse kohta – pole veel teada, aga selgub peagi);

·         Konkreetse enniku jaoks atribuut ei kehti (aadressis puudub korterinumber, sest kodanik X elab talus).

Üldiselt on NULL-väärtused andmebaasis segadust tekitavad ja parem on neid vältida. Näiteks kui kahel üliõpilasel aadress on NULL, siis kas nad elavad samal aadressil?

KITSENDUSED (constraints)

Andmetel andmebaasis on piirangud, mis tulenevad nn minimaailma "mängureeglitest". Ühes relatsioonis (tabelis) olevad kitsendused (constraints) andmetele sätestati atribuudi andmetüübiga ja vajadusel täiendavate kirjeldustega, formaatidega jne. Tabelite vahelised seosed tulenevad tabelis olevatest andmetest ja ka siin kehtivad mitmed kitsendused, mis määratakse relatsioonilise mudeliga. Kitsendusi võib jaotada kolme liiki:

·         Andmemudelist tulenevad kitsendused (model-based ehk implicit constraints) – nn seesmised kitsendused: andmemudeliga on tüüpiliselt  määratud, et samasugune ennik ei tohi korduda samas tabelis.

·         Andmemudeli skeemiga esitatavad kitsendused (schema-based ehk explicit constraints) – nn ilmutatud kitsendused ehk relatsioonilises mudelis esitatavad kitsendused.

·         Kitsendused, mis tuleb realiseerida rakenduses (semantic constraints ehk business rules). Ärireeglid on erinevad kokkulepitud (või ka kokkuleppimata) põhimõtted, mida tuleb järgida nii inimestel kui ka tarkvaral. Need on võimalik kehtima programmeerida enamasti rakenduse tasemel.

 

SEESMISED KITSENDUSED: DOMEENI KITSENDUSED

Domeeni ehk määramispiirkonna kitsendused (domain constraints):

·         Iga atribuudi väärtus on atomaarne ehk mittejagatav.

·         Domeeniga seotud atribuudid on tavapärased: arvulised väärtused int ja real (float), märgid, stringid, ajad, kuupäevad, ... Konkreetsed andmetüübid koos oma loomulike piiridega erinevad erinvates andmebaasihalduse süsteemides mingil määral

·         Domeeni väärtuseid võivad kitsendada ka vahemikud andmetüübi sees (nt vanusevahemik), loetelutüüp (enumerated type) koos etteantud väärtuste loeteluga (nt nädalapäevad).

 

KITSENDUSED VÕTMETELE

Kaks rida ühes tabelis ei tohi olla täpselt ühesugused. (mat: Relatsioon on hulk, hulga kõik elemendid peavad olema erinevad)

Tavaliselt kehtestatakse erinevuse nõue osadele atribuutidele, mille väärtuste kombinatsioonid ei tohi erinevatel ridadel korduda. Sellist atribuutide kombinatsiooni nimetatakse supervõtmeks (superkey). Supervõtmega määratakse unikaalsuse kitsendus (uniqueness constraint) ehk supervõtmete erinevuse nõue üle kõigi ridade ühes tabelis. Kui supervõtmes võib olla ka atribuute, mis on unikaalsuse määramiseks ülearused (atribuudi eemaldamisel unikaalsus säilub), siis võti (key) on minimaalne atribuutide kombinatsioon, mis on ühene, kuid samas ei ole seal ülearuseid atribuute.

Võtmete unikaalsuse kitsendus peab olema tabelis täidetud igal ajahetkel, s.t.  ka tabelisse andmete lisamisel peab see nõue täidetuks jääma. Primaarvõti (primary key) valitakse välja tabeli kõigi võtmete hulgast. Ta võiks koosneda ühest atribuudist ja teda kasutatakse edaspidi ridade eristamiseks.

Primaarvõti võib olla loomulik võti (natural key) või surrogaatvõti (surrogate key):

·         Loomulik võti on tabelis olemas ja on seotud vastava olemiga.

·         Surrogaatvõtme väärtused genereeritakse andmebaasis automaatselt ja need ei iseloomusta tegelikult vastavat olemit. Ilus sõna oleks ka asendusvõti.

KITSENDUSED NULL-VÄÄRTUSTE KASUTAMISEL

·         NULL on väärtus, mis märgib tegeliku väärtuse puudumist.

·         NULLil võis olla mitu tähendust.

·         On võimalik kehtestada, et atribuudil ei ole NULLväärtused lubatud. Enamasti on seda mõistlik teha. NULL-väärtuse lubamine on pigem erandlik.

 

TERVIKLUSE KITSENDUSED

Andmed peavad olema korrektsed nii ühes tabelis kui ka kõigis tabelites kokku. Andmete tervikluse (integrity) all mõistetakse nende õigsust, asjakohasust igal ajahetkel ja nende pärinemist usaldusväärsetest allikatest. Relatsioonilises mudelis eristatakse järgmiseid kitsendusi:

·         Olemi terviklus (entity integrity) – primaarvõtmel ei tohi olla NULL-väärtust.

·         Viidete terviklus (referential integrity) – kui üks relatsioon viitab teisele relatsioonile, võib ta viidata vaid olemasolevale kirjele.

VÕÕRVÕTMETE KITSENDUSED

Relatsiooni võõrvõti (foreign key) on ühe relatsiooni atribuut, mis viitab teisele relatsioonile. Kehtivad reeglid:

·         Võõrvõtmel ühes relatsioonis on sama domeen (määramispiirkond) kui primaarvõtmel teises relatsioonis. Ehk sisuliselt nad peavad esindama nö sama asja.

·         Võõrvõtme väärtus peab võrduma mõne primaarvõtmega teises relatsioonis. Või on tema väärtuseks NULL. Täpsustatult viitavad üksteisele ennikud (kirjed) ja öeldakse, et üks ennik viitab teisele ennikule.

Kui eelnevad reeglid on täidetud, siis viidete terviklus kehtib.

TEISENDUSALGORITM

Mõistetest: ehkki relatsiooniteoorias kasutatakse mõistet relatsioon tähistamaks olemite kogumit (andmebaasi tabelit), võib lihtsustamise eesmärgil kasutada järgnevas mõistet tabel.

Konteptuaalsel mudelil on olemite struktuuri kirjeldavad olemitüübid ja olem on konkreetne eksemplar. Seitsmest sammust koosnev algoritm annab juhiseid olem-seos mudeli tabeliteks teisendamiseks ja tegeleb järgmiste kontseptuaalse mudeli osadega:

–        Olemitüübid (tugevad ja nõrgad)

–        Binaarsed seosed, millega seotakse kaks olemitüüpi.

–        Seosed, mille aste on suurem kui kaks (nendega seotakse rohkem olemitüüpe).

–        Erinevad olemitüüpide atribuudid: liht-, liit- ja mitmeväärtuselised.

TEISENDUSE 1. SAMM

Tugevad olemitüübid (regular/strong entity type): Iga tugeva olemitüübi jaoks moodustatakse tabel, mis sisaldab tema kõiki lihtatribuute. Liitatribuutide jaoks lisatakse nende lihtkomponendid (nimi → eesnimi ja perekonnanimi). Mitmeväärtuseliste atribuutide lisamist käsitleb 6. samm. Üks võtmeatribuutidest tuleb määrata primaarvõtmeks.

Tugeval olemitüübil on olemas võtmeks sobiv atribuut ja nad eksisteerivad ning on identifitseeritavad iseseisvalt. Vastandiks on nõrk olemitüüp (weak entity type), mille olemeid saab identifitseerida mõne teise olemitüübi kaudu. Öeldakse, et nõrka olemitüüpi omab mingi teine olemitüüp (owning entity type).

 

TEISENDUSE 2. SAMM

Nõrgad olemitüübid (weak entity type):  Iga nõrga olemitüübi jaoks tuleb teha tabel, millesse lisada kõik olemitüübi lihtatribuudid ning liitatribuutide lihtkomponendid.  Lisaks tuleb luua seos teda omava (ja üheselt identifitseeriva) olemitüübiga. Selleks lisa tabelisse võõrvõtmetena omava olemitüübi primaarvõti. NB! Omavaid olemitüüpe võib olla ka mitu.

Selgitus: kuna nõrka olemit ei saa üheselt identifitseerida üksnes tema enda kaudu, vaid seda saab teha läbi seose teise, teda omava olemitüübiga, siis tuleb kuidagi luua seos nende vahele – nõrga olemitüübi sisse tuleb lisada viide teda omavale olemitüübile.

 

TEISENDUSE 3. SAMM

3. sammu alguseks on eeldatavasti kõik olemid tabelitena välja joonistatud. Nüüd võib tekkida vajadus nii atribuutide lisamiseks olemasolevatesse tabelitesse kui ka uute tabelite tegemiseks. Binaarne üks-ühele seos (1:1):  Teisendamiseks on mitu võimalust:

·         Võõrvõtme kasutamine (enim kasutatav)

·         Tabelite ühendamine

·         Seos viidete abil ehk seosetabeliga.

Selgitus: 1:1 seose puhul vastab ühele ühe olemitüübi olemile maksimaalselt üks teise olemitüübi olem (ühel instituudil on antud hetkel üks isik direktoriks). Selles seoses ei pea tingimata osalema kõik olemid ühelt ja teiselt poolt. Ehk teisisõnu ei pea eksisteerima täielik osalus (total participation) mõlema olemitüübi poolt (üks ei saa olemas olla teiseta).

Võõrvõtme kasutamine (foreign key approach): Võtame ühe seoses osaleva olemitüübi ja lisame tema primaarvõtme võõrvõtmeks teise olemitüübi jaoks tehtud tabelisse (mis on eeldatavasti 1. või 2. sammu jooksul tekkinud).

Mõistlik on lisada võõrvõti selle olemitüübi tabelisse, mille osalus seoses on täielik ehk iga olem on seotud teise olemiga (sellega väldime NULL-väärtuseid).

Lisaks lisatakse atribuutidena samasse tabelisse ka seose küljes olevad atribuudid.

Tabelite (kahe olemitüübi) ühendamine (merged relation approach): See lähenemine tähendab, et kaks tabelit ühendatakse üheks tabeliks. Kasutada on mõistlik vaid juhul, kui üks olemitüüp ei saa eksisteerida teiseta ehk mõlemalt poolt on osalus seoses täielik (mõlemas tabelis on samapalju kirjeid, kui tekib ühte tabelisse kirje juurde, siis lisandub kirje ka teise tabelisse).

Seos viitega ehk seosetabeli kasutamine (cross reference / relationship relation):  Seose jaoks lisatakse uus tabel, kuhu atribuutideks lisatakse seostatavate olemitüüpide primaarvõtmed ja vajadusel veel atribuute, mis seost iseloomustavad (kuupäevad jms).

Seostatavate olemitüüpide tabeleid ei muudeta. Seda varianti võib kaaluda siis, kui kummalgi seose poolel ei ole olemitüüpide osalus täielik ning võõrvõtme lisamine ükskõik kummale poole põhjustab paljudes kirjetes NULL-väärtuse tekkimist (palju on suhteline, otsustamisel peaks aitama kogemus).

Sisuliselt kasutatakse sarnast varianti, mis on vajalik binaarse M:N ehk mitu-mitmele seose korral.

 

TEISENDUSE 4. SAMM

Binaarne üks mitmele seos (1:N):  Seose teisendamiseks on kaks erinevat juba eelnevalt kirjeldatud võimalust:

·         Võõrvõtme kasutamine

·         Seos viitega ehk seosetabeliga.

Selgitus: üks mitmele seose puhul võib vastata ühele olemile ühest olemitüübist mitu olemit teisest olemitüübist.

Võõrvõtme kasutamine: Ühte seoses osalevasse olemitüübi tabelisse lisatakse võõrvõtmeks teise olemitüübi primaarvõti. Võõrvõti lisatakse tabelisse, mis on seose mitmeses otsas.  Vastupidine võõrvõtme lisamine põhjustaks mitmeväärtuselise atribuudi tekke. Sobib kasutada, kui seose mitmeses otsas on täielik osalus – kõigil olemitel on vaste teises olemitüübis.

Seos seosetabeliga:  Lisatakse uus tabel, kus on võõrvõtmeteks mõlema seoses osaleva olemitüübi primaarvõtmed ning lisaks atribuudid, mis olid lisatud seosele.  Variant on soovitatav siis, kui seose mitmeses otsas ei ole täielikku osalust ning võõrvõtme kasutamisel tekivad NULL-väärtuseid võõrvõtme välja.

 

TEISENDUSE 5. SAMM

Binaarne mitu mitmele seos (M:N): Ainus võimalus on seos viitega ehk seosetabeliga.  Iga binaarse M:N seose jaoks tuleb luua eraldi tabel.  Võõrvõtmetena lisatakse mõlema seoses osaleva olemitüübi primaarvõtmed, millede kombinatsioon peaks olema unikaalne (ja sobima seeläbi koos seosetabeli primaarvõtmeks). Atribuutideks lisatakse kõik vastava seose lihtatribuudid ja liitatribuutide lihtkomponendid.

 

TEISENDUSE 6. SAMM

Mitmeväärtuselised atribuudid (multivalued attributes):  Mitmeväärtuselised atribuudid võiksid olla äratuntavad nimes kasutatava mitmuse kaudu ja peaksid olema ka märgitud mudelis topeltjoonega.

Iga mitmeväärtuselise atribuudi jaoks tuleb teha eraldi tabel. Uues tabelis peab olema vähemalt kaks atribuuti: üks atribuudi ühe väärtuse jaoks ja teine võõrvõti (vastava olemitüübi primaarvõti). Kui olemi mitmeväärtuselisel atribuudil on näiteks kolm väärtust, siis tekib tabelisse kolm kirjet.

Sõltuvalt mitmeväärtuselise atribuudi iseloomust ja erinevate võimalike väärtuste arvust võib siiski osutuda otstarbekaks lisada need erinevate tõeväärtustüüpi atribuutidena olemitüübi enda tabelisse.

TEISENDUSE 7. SAMM

Seosed, mille aste on suurem kui kaks (N-ary relationship):

·         Iga seose jaoks tehakse uus tabel.

·         Lisa tabelisse võõrvõtmetena kõigi seoses osalevate olemitüüpide primaarvõtmed (neid peaks siis antud juhul olema rohkem kui kaks ehk sama palju kui on olemitüüpe).

·         Kui seosel on veel lisaks atribuudid, siis lisa ka need.

·         Erinevus binaarsest mitu-mitmele seosest on see, et seosega ühendatakse mitte kaks, vaid rohkem tabeleid.

 

ANDMEMUDELI NORMALISEERIMINE. ERINEVAD NORMAALKUJUD

Kõigepealt uuesti mõisted:

·         Olem  –  üks konkreetne olemieksemplar oma atribuutide väärtustega.

·         Olemitüüp -  olemi ja tema atribuutide kirjeldus kontseptuaalses mudelis.

·         Tabel – andmebaasikirjelduses olev tabel (teoorias ka relatsiooniline muutuja, relatsioon), tabeli kirjeldus.

·         Kirje – rida tabelis ehk üks konkreetne olem.

·         Primaarvõti (primary key) => PK - kandidaatvõti, mis on valitud relatsiooni kirjeid unikaalselt identifitseerima. Primaarvõti on võti, mis üheselt identifitseerib ühe kirje. Valiku kriteeriumid:

→     atribuudi domeen (peaks olema võimalikult lühike väärtus);

→      atribuutide arv (peaks olema võimalikult vähe atribuute);

→      tulevane unikaalsuse tõenäosus (peaks sisaldama unikaalseid väärtusi nii praegu kui ka tulevikus).

·         Välis-/Võõrvõti (foreign key) => FK - seose loomiseks kahe relatsiooni vahele "tõmmatakse" ühe relatsiooni ühe (või ka mitme) atribuudi andmed teise relatsiooni salvestamiseks. Ühelt poolt peab suhte loomisel osalema unikaalne võti (mõni kandidaatvõtetest). Enamasti on selleks unikaalseks võtmeks primaarvõti. Selle tulemusel on kahes erinevas relatsiooni ühesuguse sisuga atribuudid, mis loovad suhte nende relatsioonide vahel. Seotud relatsiooni tekkinud atribuuti (atribuute) nimetatakse välisvõtmeks. Relatsioonis võib olla üks või mitu välisvõtit. Relatsioonis võib välisvõti ka puududa.

·         Normaalkuju (normal form) => NF

NB! Andmemudel peab olema lihtsalt arusaadav, võimalikult väheste lisaselgitustega, sellele aitab kaasa läbimõeldud nimede valik ning olemitüüpide mõistlik piiritlemine.

LIIGNE INFORMATSIOON KIRJETES (redundancy)

Liigne informatsioon kirjetes (redundancy) põhjustab mitmeid probleeme – näiteks raiskab mälu, võib tekitada probleeme andmete muutmisel. Mudelit koostades tuleb mõelda peamiste tabelite mälukasutuse minimeerimisele. Atribuudid tuleb olemitüüpide vahel mõistlikult jagada. Liiane informatsioon põhjustab hälbeid (anomaaliaid) lisamisel, kustutamisel ja muutmisel. Soovitus: kavandada mudel nii, et neid anomaaliaid ei tekiks. Kui nad siiski on (nt päringute kiirendamiseks), siis tuleb nad täpselt dokumenteerida.

 

ANOMAALIAD

Andmebaasimudelites esineb  lisamise, kustutamise ja muutmise anomaaliaid (insertion, deletion and modification anomalies):

·         Lisamise anomaalia: ühe olemi andmeid ei saa lisada teiseta (näitlejat filmita) ja samu andmeid tuleb korrata. Kui lisada vaid näitleja, tekivad NULLid filmi kohale. 

·         Kustutamise anomaalia: kui on vaja ühe olemi andmed kustutada, siis mis saab teisest samas tabelis olevast? Mida teha, kui tekib soov kustutada ühe näitleja andmed? Esiteks on ta mitmes kirjes ja teiseks võib kaduda ka film. 

·         Muutmise anomaalia: vajadus muuta andmeid mitmes kirjes - igal pool, kus vastava näitleja (või filmi) andmed esinevad.

NULL-VÄÄRTUSED KIRJETES

Olemitüübis / tabelis on palju atribuute, kuid osa atribuute ei kehti kõigile kirjetele. Tulemuseks on nende atribuutide NULLväärtused kirjetes. Probleemid: mälu raiskamine, atribuutide mittemõistmine, segadused JOIN-iga, ennustamatud võrdlemiste ja agregaatfunktsioonide tulemused. NULL-väärtusel võivad olla erinevad põhjused:

·         Konkreetsel kirjel puudub see atribuut;

·         Kirje atribuudi väärtus ei ole teada ja ei selgu ka edaspidi;

·         Kirje atribuudi väärtus ei ole veel teada, kuid edaspidi selgub.

Soovitus: NULLe tuleb vältida, kui vähegi võimalik. Selleks:

·         vähenda NULL-ide kasutust,

·         kui paljudes kirjetes tuleb mõne välja väärtuseks NULL, tee eraldi tabel kirjetele, kus vastav atribuut ei ole NULL ning ühenda võõrvõtit kasutades põhitabeli kirjetega,

·         kui NULL on vältimatu veendu, et seda kasutatakse vaid eriolukordades ja erista vajadusel erinevad NULL-i variandid,

·         NULLid eriolukordades on kasulik ka dokumenteerida.

 

LIIGSED JA VÕLTSID KIRJED

 

Kui ühendada kirjeid erinevatest tabelitest läbimõtlematult valitud väärtuste järgi, võib saada uued kirjed, mis on sisuliselt valed ning kus olev info ei ole kooskõlaline. Kui JOIN teha PK-d ja FK-d aluseks võtmata, sai hulkade korrutise (Cartesiuse korrutise), milles ühendati kõik kõigiga. Selline olukord võib olla järjeks varem tehtud atribuutide sobimatule jaotusele erinevatesse tabelitesse. Näiteks kui lööksime filmistaaride tabeli suvaliselt pooleks nii, et näitleja 3 veergu jäävad ühte tabelisse ja ülejäänud väljad teise tabelisse.

Soovitus: koosta mudel nii, et seosed tekiksid läbi atribuutide väärtuste võrdumise ning välistaksid võltside kirjete (spurious tuples) tekkimise. Seosed tuleb soovitavalt luua PK ja FK abil (primaar- ja võõrvõtmetega).

 

VÕTMETELE TUGINEVAD NORMAALKUJUD

Andmemudeli normaliseerimist kirjeldas esimesena Edgar F. Codd aastal 1972.  Normaliseerimis-protsessi käigus testitakse andmemudeli vastavust mingile normaalkujule. Selleks analüüsitakse seoseid PK-de ja FK-de kaudu.  

·         Eesmärk: minimeerida informatsiooni liiasus, minimeerida lisamise, kustutamise ja muutmise anomaaliad.

·         Kaugem eesmärk: vähendada vigu andmemudelis, mis hiljem end kurjalt kättemaksma hakkavad. Kui mudel ei läbi normalkujude teste, tuleb olemeid tükeldada.

 

VÕTMED

·         Primaarvõti (primary key) valitakse välja kandidaatvõtmete hulgast (subjektiivne otsus) ning määratakse eristama tabelis olevaid kirjeid.  Primaarvõti võib hõlmata mitut atribuuti, s.t. olla liit- / komposiitvõti (composite key). Teised kandidaatvõtmed on alternatiivvõtmed.

·         Surrogaatvõti (surrogate key) on atribuut, mida saab kasutada primaarvõtmeks:

– hõlmab vaid ühe atribuudi.

– tal ei ole kasutaja jaoks sisulist tähendust.

– uue kirje lisamisel kasutatakse võtme väärtust, mida pole kunagi enne selles atribuudis kasutatud (kustutatud kirje võtit ei kasutata uuesti).

– enamasti genereeritakse väärtused automaatselt.

·         Võõr- /välisvõti (foreign key), ka välisvõti on tabeli atribuut, mis vastab teise (või sama) tabeli kandidaatvõtmele.

– Enamasti on tegemist teise tabeli primaarvõtmega.

– Võõrvõtmete abil seotakse tabelid.

– Viidete terviklikkuse reegel (referential integrity) ütleb, et kirje ühes tabelis, mis viitab kirjele teises tabelis, peab viitama olemasolevale kirjele. Teisisõnu võõrvõtme väärtusele peab vastama teises tabelis mingi kirje kandidaatvõtme (enamasti primaarvõtme) väärtus.

PROBLEEMID NORMALISEERIMATA KUJUS

Üheks normaliseerimata kuju tunnuseks on korduvgruppide esinemine. Korduvgrupiks nimetatakse mingi hulga atribuutide kordumist tabeli kirjelduses (ja ka kirjes) – näiteks tabelisse Arve on lisatud atribuudid 5 rea lisamiseks arvele.

·         Lisamise anomaalia – korduvgruppide arv on piiratud – nt 5 rida arvel. Aga kui soovitakse rohkem kaupa?

·         Kustutamise anomaalia – ühe korduvgrupi kustutamine kirjest tekitab “augu”;

·         Info liiasus – kui sama element on mitmes korduvgrupis (erinevates kirjetes), tuleb teise kirjesse lisada kõik andmed, mis on juba esimese olemas;

·         Uuendamise anomaalia – tuleneb eelmisest – uuendada tuleks igal pool, ei piisa ühes kirjes muudatuste tegemisest;

·         Andmete ebaadekvaatseks muutumine – mõned kohas jäävad andmed uuendamata;

·         Mälu raiskamine – ühelt poolt korduv info, teisalt tühjad väljad korduvgruppides.

 

1 NF - ESIMENE NORMAALKUJU

1NF  keelab mitmeväärtuselised atribuudid, liitatribuudid ja nende kombinatsioonid. Iga atribuudi võimalikus väärtuste hulgas on vaid mittejagatavad (atomaarsed - atomic) väärtused vastavast väärtuste hulgast.

1NF keelab atribuutidele panna väärtuseks hulkasid, kirjed (tuple) ja nende kombinatsioone. Lisaks peavad ühes veerus olema ühte tüüpi väärtused ning veergudel (atribuutidel) selged eristuvad nimed. Mitmeväärtuselise atribuudi näiteks on filmi žanr. Mitu kirjet (tuple) atribuutidena - selle näiteks võiksid olla arvel korduvad read, mida püütakse arve teiste andmetega samasse tabelisse paigutada.

TEISENDUS:

Kolm peamist võimalust mitmeväärtuselise atribuudi või ka mitme korduva atribuutide grupi (tuple) jaoks.

1)      Eralda mitmeväärtuseline atribuut või korduv kirje teise tabelisse. Lisa talle võõrvõtmeks seotud kirje primaarvõti. Kui näiteks on atribuudil 3 väärtust, siis tekib 3 kirjet.

2)      Mitmeväärtuselise atribuudi erinevate väärtuse või iga korduva atribuutide grupi jaoks moodustame eraldi kirjed, ülejäänud väljade väärtused korduvad (tekib andmete liiasus).

3)      Kui on teada mitmeväärtuselise atribuudi või korduvate kirjete maksimaalne väärtuse arv, võib teha tabelisse ka vastav arv väljasid. Kuid sel juhul riskitakse NULL-väärtustega mitmetes väljades.

NF 1 sisaldab jätkuvalt mitmeid probleeme. Tabelis võib tekkida transitiivne seos – ehkki on üks primaarvõti, on tabelis koos erinevate andmeobjektide atribuudid ja vaid osad nendest on seotud PK-ga, teised aga omavahel. Tabelis võib olla jagatud võti (kui PK koosneb mitmest atribuudist). Üks osa võtmest on seotud rohkem ühe osa atribuutidega ja teine võti teise osa atribuutidega. Erinevate andmeobjektide väljad ühes tabelis (kirjes) põhjustavad probleeme nii andmete lisamisel kui kustutamisel – andmeid saab lisada vaid paarina. Anomaaliad on valdavalt alles.

 

FUNKTSIONAALNE SÕLTUVUS:

Ühes tabelis võivad olla sõltuvused atribuutide vahel. Funktsionaalse sõltuvuse (functional dependency) mõistet kasutatakse 2NF  kirjeldamiseks ja sellele üleminekuks.

Kui ühes relatsioonilises muutujas (tabelis) olev atribuutide hulk A sõltub samas muutujas (tabelis) olevast atribuutide hulgast B, on tegemist funktsionaalse sõltuvusega.

Atribuut A identifitseerib üheselt atribuudi B (A → B, A määrab B, B sõltub Ast). Võib ka mõelda nii, et atribuudid on omavahel sõltuvuses siis, kui nad on seotud ühe andmeobjektiga. Eespool olnud näide Filmistaari tabeli kohta, kus omavahel olid sõltuvuses näitleja andmed ja teise sõltuvusena filmi andmed. 1NF ei keela näiteks sellist tabelit.

2 NF – TEINE NORMAALKUJU

2NF baseerub  täielikul funktsionaalsel sõltuvusel, mis tähendab atribuutide hulka, kust ei saa enam ühtegi atribuuti eemaldada, sest nad kõik on omavahel seotud, eemaldamisel kaob midagi olulist. Relatsioon (tabel) on teisel normaalkujul, kui ta on 1NF kujul ja iga atribuut, mis ei ole PK, on funktsionaalselt täielikult sõltuv relatsiooni (tabeli) primaarvõtmest. Ühes relatsioonilises muutujas olevad atribuudid peavad olema üheselt seotud terve primaarvõtmega (mitte selle osaga, kui primaarvõti koosneb mitmest atribuudist ehk on tegemist jagatud võtmega).

Teisendamiseks 2NF vormi tuleb tabel tükeldada (dekompositsioon) mitmeks tabeliks, lähtudes funktsionaalsest sõltuvusest. Dekompositsiooni aluseks on erinevate atribuutide sõltuvus jagatud primaarvõtme osadest.

Kui suudame määrata tabelis funktsionaalsed sõltuvused, siis igaühe jaoks nendest tuleb teha uus tabel. Igal funktsionaalsel sõltuvusel on oma osa PK-st.

Teise tabelisse tõstetavatele atribuutidele vastav osa võtmest saab uue olemi PK-ks. Algses tabelis muutub sama võtme osa FK-ks, mis tagab seose uue tabeliga.

NB! Tabeleid tükeldades ei tohi kaotsi minna seosed!

2 NF NÄIDE (Elmasri & Navathe):

 

Tabelid kirjeldatud päiste kaudu, FD1, FD2, FD3 on funktsionaalsed sõltuvused, igast sõltuvusest saab tabeli. SSN - isikukood, Pnumber - projekti number, Hours – projektiga töötatud tunnid, Ename – töötaja nimi, Pname – projekti nimi, Plocation – projekti asukoht

Mida näeme? Kadunud on jagatud võtmest tingitud anomaalia: näiteks vajadus lisada kahte erinevat andmeobjekti korraga ühte kirjesse, sest erinevate objektide andmed on erinevates tabelites. Säilunud on transitiivsest seosest tingitud anomaaliad:

→     võtmega mitteseotud andmeid ei saa sõltumatult lisada;

→     kustutades PK-ga seotud andmed, kaovad ka temaga ülekanduvalt seotud andmed;

→     PK-ga mitteseotud andmed korduvad kirjetes: andmeliiasus + muutmise anomaalia + andmete ebaadekvaatseks muutumine.

3 NF – KOLMAS NORMAALKUJU

3 NF saadakse, kui 2 NF-st kaotatakse transitiivsed (ülekanduvad) seosed. Transitiivne seos (transitive dependency) on selline funktsionaalne seos atribuutidel X ja Y (X→Y), kus eksisteerib atribuut Z nii et kehtivad seosed X→Z ja Z→Y. Sealjuures Z ei ole ei kandidaatvõti ega osa ühestki võtmest. 3NF-s on PK-sse mittekuuluvad atribuudid vastastikku sõltumatud ehk muuta võib ühe atribuudi väärtust teise väärtust muutmata. 

E. F. Codd’i algse definitsiooni kohaselt: relatsioon (tabel) on 3NF, kui ta rahuldab 2NF tingimusi ja ükski relatsiooni mitte-PK atribuut ei ole transitiivses sõltuvuses PK-st.

NÄIDE

Järgnev tabel (Elmasri & Navathe) on 2NF. Ehkki tabelis on  erinevate andmeobjektide andmed (Employee ja Department), ei ole nad sõltuvuses jagatud PK erinevatest osadest. Puudub üldse jagatud PK (PK-ks on vaid Ssn). Transitiivne seos, Dnumber ei ole PK osa: Ssn→Dnumber, Dnumber→Dname.

Transitiivset sõltuvust sisaldavale tabelile tehakse dekompositsioon, jagades selle mitmeks 3NF tabeliks. Uude tabelisse viiakse atribuudid, mis on PK-ga transitiivses sõltuvuses ehk ei sõltu otseselt PK-st. Uues tabelis määratakse PK, mis on unikaalne seal olevatele kirjetele. Uue tabeli PK läheb FK-ks algsesse tabelisse, kuid ei lähe sealse PK koosseisu.

Vt näidet eespool joonisel, kus Department’i andmed viidi teise tabelisse  ning Dnumber sai PK-ks ja Employee tabelis FK-ks.

3NF-le vastavates tabelites on atribuudid ühe olemi (objekti) seotud andmete salvestamiseks. Tabeli iga PK-sse mittekuuluv atribuut on funktsionaalselt täielikult sõltuv tervest PK-st. Lisamise, muutmise ja kustutamise anomaaliatest peaks 3NF-ile vastav tabel vaba olema. Esile kerkib PK uuendamise anomaalia, sest selle muutmisel on vaja muuta tema väärtust kõigis kirjetes, mis sama võtit FK-na seostamiseks kasutavad.

BOYCE-CODD’i NORMAALKUJU

Boyce-Codd Normal Form (BCNF)  on 3 NF üldistus, või veel suurem kitsendus. Relatsioon (tabel) on BCNF, kui tabeli iga atribuut sõltub täielikult kogu primaarvõtmest ja ainult primaarvõtmest. Teisisõnu BCNF-ile vastavas tabelis ei tohi olla teisi sõltuvusi, kui ainult tavalise atribuudi (non-prime attribute) sõltuvus primaarvõtmest. Enamasti tähendab üleviimine veel mingi tabeli tükeldamist ja see peaks aitama veel vähendada andmete dubleerimist, kuid vastav olukord tekib üsna erijuhtudel.

ANDMEMUDELI DENORMALISEERIMINE

Normaliseeritud andmemudelit muudetakse andmebaasi jõudluse suurendamiseks.

Jõudluse probleemid tekivad näiteks sellest, kui kõigi normaliseerimiste tulemusena on baas killustunud väga paljudeks väikesteks tabeliteks. Iga denormaliseerimise otsus peab olema kaalutletud ja seotud konkreetse andmebaasi, ärireeglistikuga, peamiste päringutega jms.

Reeglina ei minda normaliseerimisel üle 3NF-i.

Denormaliseerimise võtted:

·         Liit-atribuudid: liidetakse kokku väljad, mis reegleid järgides peaksid olema eraldi atribuutideks või ka tabeliteks, et vältida päringuid läbi mitme tabeli. Vajadus sõltub olukorrast, nt aadress personali andmebaasis või logistikasüsteemis. 

·         Andmete agregeerimine: tabelites hoitakse tuletatud atribuutide väärtuseid (keskmised, summad). Neid saab teiste atribuutide järgi alati välja arvutada, aga kui neid tihti vaja läheb, aitab see efektiivsust tõsta. Nt pangakonto saldo.

·         Gruppeerivad atribuudid:  lisatakse ID, mis ei ole primaarvõti, kuid mida kasutatakse seose loomiseks sama tabeli teiste kirjetega või teise tabeliga (nt säilitada olemi ajalugu läbi kirjete ja suuta ajaloolisi kirjeid omavahel seostada: isiku sama tüüpi töölepingu kõigile versioonidele lisatakse grupeeriv ID, isiku ID-st ei piisa – erinevat tüüpi lepingud. 

·         Koondolemid – ühte olemisse pannakse kokku mitmes olemis olevaid atribuute. Põhjuseks vajadus teha tihti vastavaid päringuid. Koondolem ei välista olemite eksisteerimist eraldi. Koondolemit ehitatakse tasapisi koos andmete tekkimise ja muutumisega.

KASUTATUD MATERJALID:

• IFI6013.DT loengumaterjalid. Andmebaaside projekteerimine. Koostanud: Inga Petuhhov. TLÜ DTI, 2019.